지금까지 우리는 두가지 모델에 대해서 배웠습니다.
Supervised Learning에 대한 Linear regression 모델과 Logistic regression 모델을 배웠습니다.
이 두가지 모델을 이용하면 상당히 많은 머신러닝에 대한 해답을 찾을 수 있을 것입니다.
Overfitting
이시점에서 우리는 h함수에 대해서 조금더 알아보도록 하겠습니다.
아래 그림은 Linear regression에서의 dataset을 그래프로 표현한 것입니다. 가장 왼쪽에 세타에 대한 1차방정식으로 h함수를 정의했다고 생각합시다. 이때 직선을 그리면 그래프와 같이 될 것입니다. 실제 데이터 결과와 직선으로 예측되는 결과와는 완전히 일치를 하지 않습니다. 대략적으로 추정이 가능한 정도의 수준입니다. 이때의 h함수를 Underfit 또는 High bias라고 이야기 합니다. 아직 덜 최적화가 되어 있어 더 최적화 할 수 있다는 의미가 됩니다.
가장 오른쪽에 그래프를 보겠습니다. 이때의 h 함수는 4차방정식으로 표현되는 다차원방정식으로 나타내었습니다. 그래프를 그리면 많은 곡선으로 이루어진 하지만 각각의 데이터 결과 값을 모두 만족하는 형태가 됩니다. 우리가 가지고 있는 샘플 dataset에서는 아주 최적화가 잘되어 있다고 생각할 수 있지만, 새로운 dataset에서도 잘 적용이 될지 즉, 일반적으로도 적용이 가능한지에 대해서는 의심스럽습니다. 이러한 h 함수가 발생하는 문제를 Overfit 또는 High variouce라고 합니다. 너무 과하게 최적화가 되어서 일반화하기 어려운 상태를 의미합니다.
가운데 그래프를 보겠습니다. 2차방정식으로 구성되어 그래프를 그리면 어느정도 dataset에 적합하면서 집값의 가격상승분에 대한 그래프를 잘 나타내어 주고 있습니다. 이것을 Just right라고 표현하고 적절한 최적화가 되었다고 할 수 있습니다.
이번에는 Logistic regression에서 동일한 방식으로 알아보겠습니다.
가장 왼쪽의 1차방정식의 경우 어느정도 가능한 예측치를 제시할 수 있기는 하지만 최적화가 덜 되었습니다.(Underfit)
가장 오른쪽의 다항식의 경우에는 너무 샘플 데이터에 대해서 과최적화가 되어 일반적으로 사용하기가 어려울 것 같습니다.(Overfit)
가운데의 2차방정식의 경우 적절한 예측치를 제시할 수 있어 좋아보입니다.
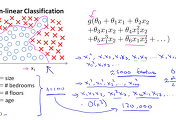
실제로 우리가 사용하게 될 dataset에는 상당히 많은 features가 포함되어 있을 것입니다.
이것을 사용하여 모델을 적용하게 되면 자연스럽게 overfitting 현상이 발생하는 경우가 생기게 됩니다.
이런 과최적화(Overfitting)를 해결하는 방법에는 2가지 옵션이 있습니다.
하나는 사용하는 features의 수를 줄이는 방법입니다. 이것은 핵심 정보를 제외하고 일부 정보를 포기하는 형태가 되는데 이것을 특별한 알고리즘을 사용해서 자동적으로 수행할 수도 있습니다. 하지만 이것은 결과에 중요한 영향을 미치는 feature가 버려지는 결과가 발생할 가능성이 있는 단점이 있습니다.
또 다른 하나는 우리가 배울 정규화(Regularization)를 사용하는 것입니다.
모든 features를 사용할 수 있으며 대신 parameters의 값과 크기를 줄이므로서 해결하는 방법입니다.
Reqularization
정규화에 대한 개념을 직관적으로 살펴보면,
아래 그림에서 왼쪽의 h 함수는 2차방정식으로 되어 있고, 오른쪽의 h 함수는 4차방정식으로 되어 있습니다. 과최적화가 된 모습이죠.
우리가 배운 Linear regression에서 Cost 함수를 그대로 사용한다고 생각하고 뒤에 세타three와 세타four를 1000으로 곱해서 추가한다고 생각해보겠습니다.
이 새롭게 추가된 Cost 함수는 minimize 세타를 찾기 때문에 세타three와 세타four의 값은 아주 작은 거의 0에 가까운 값이 될 것입니다. 결국 4차방정식의 h 함수가 뒤에 뒤에 두개 항이 0이 되므로 2차 방정식과 같아지게 됩니다. 이것이 정규화에 개념이 됩니다.
0부터 n개의 parameters가 있을때, 일부 parameter를 작은 값으로 만들면 다항식의 h 함수가 심플해지도록 할 수 있습니다. 이것이 overfitting을 적게 발생시킬 수 있으며 정규화를 한다고 이야기 합니다.
이것을 공식으로 표현을 하면 Cost함수인 J 함수뒤에 추가적인 람다의 공식을 더하여 만들수 있습니다.
람다 곱하기 i가 1부터 n까지의 합의 세타j 제곱의 형태가 되는데, 이때 i는 parameters의 수를 의미하며 세타zero는 상수항이므로 제외하고 1부터 시작해야 합니다.
이렇게 cost 함수에 regularization 식을 추가하여 아래 그림의 공식과 같이 J함수가 됩니다.
이때 람다(lamda)를 regularization parameter라고 하며 이 람다가 하는 역활은 2가지로 구분할 수 있습니다.
하나는 본래의 cost 함수가 잘 적용이 될 수 있도록 조절해주는 역활을 하며, 또 하나는 고차항의 parameters를 아주 작은 0에 가까운 값으로 만들어주어 적당한 2차항의 함수로 만들어주는 정규화의 역활을 수행합니다.
만약에, 람다의 값을 아주 큰 값으로 10에 10승의 값으로 셋팅을 했다고 생각해보겠습니다.
람다가 아주 큰 값이 되면 세타의 parameter값들이 모두 0이 되어 버려서 결국 세타zero만이 남게 되고 이것은 1차함수의 직선으로 그래프에 그릴 수 있게 될 것입니다. 이것은 dataset에 대하여 적절하지 않은 Underfit 의 함수가 되어 버리게 됩니다.
그러므로 우리는 람다의 값을 적절하게 조절을 해야하며 이것을 어떻게 셋팅하고 자동적으로 셋팅하게 할 수 있는지 더 알아보도록 하겠습니다.
Regularized Linear Regression
Linear Regression에서의 정규화에 대해 더 알아보겠습니다.
위에서 Cost 함수에 정규화식인 람다를 추가하여 정규화된 Cost함수를 생성하였습니다.
이번에는 Gradient Descent에서 세타 parameter를 업데이트하는 공식에 정규화를 적용하는 것에 대해서 알아보겠습니다.
정규화를 수행할때 세타zero를 제외하고 세타one부터 정규화를 하도록 했었죠?
그래서 세타zero는 별도로 나누어 처리하도록 하기 위해서 아래 그림의 공식과 같이 세타zero와 세터j로 구분하였습니다.
세타zero는 정규화 대상이 아니므로 그대로 두고
세타j는 정규화 대상이므로 뒤에 람다로 표현된 식을 추가해줍니다. ( lamda / m * theta j )
이 식을 정리해서 다시 쓰면 맨 아래와 같은 식으로 표현할 수 있습니다. 이때 세타j의 함수는 세타j와 (1 - alpha * lamda/m)이 되는데, 여기서 알파와 람다와 m은 모두 0보다 큰 값이므로 결국 이식의 값은 1보다 작은 값이 됩니다.
그러므로 앞의 식의 의미는 세타j를 줄여간다는(minimize)것을 알수 있습니다. 이것은 Gradient Descent 알고리즘이 하는 역할과 동일합니다.
그리고 뒤부분의 공식은 이전에 배운 Gradient Descent 의 공식 그대로 남게 됩니다. 정규화가 잘 적용이 되었습니다.
이번에는 Gradient Descent를 사용하지 않고 Normal Equation을 사용하여 처리할 때 정규화를 어떻게 하면 되는지 알아보겠습니다.
X matrix는 m by (n+1)의 크기를 갖는 메트릭스입니다. y vector는 m 의 크기를 갖는 벡터입니다.
이때 세타를 구하는 공식은 ( Xt*X) inverse * Xt*y 였습니다. Xt * X 뒤에 람다와 메트릭스를 곱한 값을 추가하면 됩니다.
이때의 matrix는 아래 그림의 파란색 매트릭스와 같이 대각선 방향으로 1을 갖으며 그외에는 0이 되고, 특히 첫번째 세타zero의 자리에는 0으로 시작됩니다. 만약, n=2인 경우에는 맨 아래의 matrix와 같이 3 x 3 크기의 matrix가 되며 [0,0,0; 0 1 0; 0 0 1] 의 값을 갖습니다.
이전에 배운것과 같이 Xt*X의 값이 non-invertibility가 되는 경우가 있었습니다.
정규화된 즉, 람다가 0보다 큰 값이라면 Xt*X가 non-invertiblilty라고 할지라도 람다식으로 인하여 항상 invertible하게 되니 걱정할 필요가 없습니다.
Regularized Logistic Regression
이번에는 Logistic Regression에 정규화를 적용하는 것에 대해서 알아보겠습니다.
아래 그림에서 처럼 과최적화가 된 h 함수가 있습니다. 그리고 Cost 함수인 J함수는 log의 함수로 나타낼 수 있었습니다.
Cost 함수 J에 정규화 식을 추가합니다. 아래 그림의 람다로 시작되는 파란색 공식입니다. 이때 역시 세타zero는 정규화에서 제외시킵니다.
이번에는 Gradient descent에 정규화를 적용해 보겠습니다.
세타zero는 정규화 대상이 아니므로 분리하여 그대로 두고, 세타j는 정규화 식을 아래와 같이 람다로 시작하는 파란색 공식을 추가하여 바꿀 수 있습니다. 이때 세타의 공식은 Linear regression에서와 동일하지만 h 함수가 sigmoid 함수로 다르다는 것을 잊지 말아야 합니다.
실제로 이것을 Octave에 구현할 때에도 앞에 알아본 것과 같이 Cost 함수(jVal) 정규화 식이 추가된 형태로 변하며, Gradient 세타에 대한 함수도 세타zero를 제외하고 정규화식이 포함되어 변하기만 하면 됩니다. 아래 그림의 식을 참고하셔서 구현해보시길 바랍니다.
'Machine Learning' 카테고리의 다른 글
| 20. 뇌신경망을 이용한 머신러닝 예제 (Neural Networks) (0) | 2016.07.21 |
|---|---|
| 19. 뇌신경망을 활용한 머신러닝 개념 (Neural Networks) (1) | 2016.07.20 |
| 17. 여러개의 결과로 분류하는 방법 (multiclass classification:one vs all) (0) | 2016.07.18 |
| 16. Logistic Regression을 처리하는 방법 (5) | 2016.07.16 |
| 15. Supervised Learning - Classification 표현 (12) | 2016.07.15 |

















댓글