Neural Networks Motivation
앞에서 배웠던 non-linear classification을 조금더 살펴보겠습니다.
2개의 features가 있을때 아래 그림의 그래프와 같이 dataset이 존재하고 이것을 곡선으로 decision boundary를 표현할 수 있습니다.
여기서 featrures가 100개로 늘어났을 경우를 생각해봅시다.
각 features의 2차항으로 h 함수를 생성한다고 가정할때 다음과 같이 각각의 곱 혹은 제곱으로 표현이 됩니다.
x12 ,x1x2, x1x4 ..., x1x100
이렇게 만들어진 features의 수는 약 5,000개가 되고 이것은 features 수가 n 개라고 할때 (n제곱 / 2) 만큼의 갯수가 됩니다.
만약 3차항의 h 함수를 생성한다고 가정하면 역시 동일하게 다음과 같이 곱 혹은 3제곱으로 표현이 되며
x12x2, x1x2x3, x1x4x23.....
이렇게 만들어지는 features의 수는 약 170,000개가 되고 (n의 3제곱) 만큼의 갯수로 늘어납니다.
그러므로 이것은 n의 수가 큰 dataset을 다루기에 용이하지 않습니다.
우리는 아래 그림의 이미지를 보면 차라는 것을 바로 알지만,
컴퓨터는 이미지의 데이터들을 수치로 보게 됩니다. 차 문의 손잡이 부분을 컴퓨터가 보는 방식으로 보면 matrix형태의 각 픽셀별로의 다양한 색상에 대한 데이터로 표현이 될 것입니다.
왼쪽에 자동차 사진을 주고 오른쪽에 자동차가 아닌 사진을 주고 테스트를 한다고 했을때 우리는 자동차라는 것을 바로 알 수 있지만, 컴퓨터도 이들 사진들을 학습하여 자동차라는 정답이 나오도록 해야 할 것 입니다. 이것이 Computer Vision의 한 예시입니다.
그럼 컴퓨터는 어떻게 시각적인 이미지를 판단할 수 있을까요
이미지에서 특정 부분의 픽셀들을 분석하여 학습을 하게 될 것입니다. 이 학습 결과를 통해서 이 이미지는 자동자인지 아닌지를 판단(Classification)하게 되겠죠.
이렇게 이미지들을 학습하여 Decision Boundary가 아래 그림과 같이 곡선으로 생성이 되었다고 합시다.
일단 이 곡선은 non-linear 하고 이때의 이미지가 50 x 50의 크기를 갖는다고 하면 우리는 2,500 pixels에 대해서 처리를 해야 하게 됩니다. 만약 이미지가 RGB의 칼라이미지라고 하면 더 많은 7,500개의 features가 발생을 하기 때문에, 가능하면 gray 톤으로 처리해야 칼라보다 적은 features로 학습이 가능할 겁니다.
Neural Networks 개요
머신러닝에서의 Neural Networks는 사람의 뇌 구조와 비슷하게 만들어졌습니다. 그래서 이런 뇌신경망을 이용한 알고리즘들이 생겨나고 이것을 Deep Learning이라고 불립니다.
8, 90년대부터 시작되어 현재까지 발전되어 왔으며 이 시대의 저명한 교수님들이 현재 미국과 캐나다에서 왕성하게 활동중이십니다. 이런 기술들은 현재 많은 분야에서 최첨단의 기술로 재기되고 있습니다.
사람의 뇌에 대한 연구에서 재미있는 것은
귀를 통해 소리를 처리하는 뇌 부분에 귀와 연결된 선을 제거하고, 눈과 연결된 선을 이어주면
해당 청각 피질이 볼수 있게 된다고 합니다.
이것은 뇌의 특정 부위가 특정한 처리를 담당하는 것이 아니라, 그 부위가 그렇게 사용되고 있기에 그런 역할을 하고 있는 것이라고 생각할 수 있습니다. 뇌가 어떤 입력 데이터에 대한 학습에 따라 발전한다는 의미입니다.
그래서 다양한 실험들이 있었다고 합니다.
혀를 통해 볼수 있는 실험을 하고 시각장애자가 어떤 소리에 대한 반응(sonar)을 통해서 운동도 하고 볼수 있게 되는 것이 가능하다고 합니다. 뇌는 정말 신비한 것 같습니다.
사람의 뇌는 뉴런이라는 세포로 구성이 되어있습니다.
이 뉴런은 아래 그림과 같이 Dendrite 라고 하는 부위에서 어떤 input 정보를 받고 이것을 계산하여 Axon이라는 부위를 통해 다른 뉴런에게 output 정보를 보냅니다.
이러한 뉴런이 여러개가 모여서 A뉴런은 받은 정보를 처리하고 다른 B뉴런에게 전달하고, B뉴런은 또 다른 C뉴런에게서 받은 정보를 처리하고 A뉴런에게서 받은 정보 결과와 함께 다른 D뉴런에게 결과를 전달하게 됩니다.
이러한 뉴런의 구조를 Logistic unit으로 표현을 할 수 있습니다.
아래 그림에서와 같이 x1, x2, x3의 3가지 input 정보가 있고 이것을 처리하여 h 함수의 결과가 되는 것이지요.
이때 Xzero는 1의 값을 갖는 상수임으로 표현을 할 수 있고 때로는 생략을 할 수도 있습니다. 이것을 bias unit이라고 합니다.
3개의 input과 1개의 output을 갖는 이 unit의 결과인 h 함수는 sigmoid(logistic) 함수라고 했었죠?
Neural Networks에서는 이 함수를 activation function이라고도 부르며, 세타는 parameters 라고 불렀었는데 이것도 가능하고 weights 라고 불리우기도 한다고 합니다.
이번에는 좀더 복잡하게 구성이 되어 있습니다.
Layer라는 개념이 추가되어 3개의 Layer로 구성이 되어있습니다.
Layer 1은 input 데이터를 받는 부분이므로 Input layer라고 하며, Layer 3는 output 데이터를 전달하는 부분이므로 output layer라고 합니다. 그리고 중간에 있는 Layer 2는 hidden layer라고 합니다. 그냥 데이터를 input하거나 output하지 않는 부분이라 명칭이 그러합니다.
이 구성을 수학적으로 표현을 하면 아래 그림과 같습니다.
3개의 units과 3개의 layers로 구성이 되어 있는 Neural Network입니다.
각각의 unit은 activation unit으로 a라고 표현을 하며, 이 때 사용되는 데이터에 대한 martrix를 Theta로 표현을 하기로 합니다.
첫번째 layer의 unit들은 순서대로 a11, a21 and a31 와 같이 표현이 되며, 두번째 layer의 unit들은 a12, a22 and a32
, 세번째 마지막 layer는 a13 로 표현할 수 있습니다.
그리고 Ɵj 는 layer j에서 layer j+1로 전달되는 weights의 matrix를 표현합니다. 여기서 j layer가 Sj units을 가지고 있고 j+1 layer가 Sj+1 units을 가지고 있다고 하면 이때 Theta j 의 크기는 Sj+1 x (Sj + 1) 이 된다는 것을 기억해줍니다.
Layer 1에서 Layer 3으로 진행이 되는 것을 Forward propagation 이라고 합니다.
여기서 Hidden Layer인 layer 2에서의 a unit은 theta * x 들의 합으로 되어 있으며 이것을 z라고 놓으면, a2(2)는 g( z(2) )로 표현할수 있습니다. 이와 같이 각각의 unit을 아래 그림과 같이 표현 할 수 있습니다.
그렇게 최종 결과값인 h 함수는 a(3)의 unit과 같으며 g( z(3) )과 같습니다.
Layer 1에서 x1, x2, x3의 입력 값을 받아서 Theta(1)의 matrix로 Layer 2에게 전달이 되며 이때 2차항의 feature가 될 수 있게 됩니다. 그렇게 Layer 2에서 또 다시 연산이 되어 Layer 3로 전달이 되고 최종 결과값인 h 함수가 처리가 됩니다.
이때 h 함수는 파란색으로 표현된 공식과 같이 Theta와 a의 곱에 대한 합으로 나타나며 이 값을 g의 함수로 감싸서 생성이 됩니다.
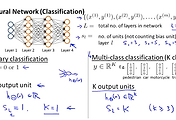
이러한 Neural Networks는 다양한 units 크기와 다양한 layers로 구성이 될 수 있으며
이런 도면과 같은 형태를 architecture 라고 합니다. 아래 그림의 구성은 4개의 Layer로 구성이 되어 있으며 hidden layer가 2,3 두개로 구성이 되어 있음을 알수 있습니다.
'Machine Learning' 카테고리의 다른 글
| 21. 뇌신경망을 이용한 머신러닝 (Neural Networks) Cost & BP (4) | 2016.07.22 |
|---|---|
| 20. 뇌신경망을 이용한 머신러닝 예제 (Neural Networks) (0) | 2016.07.21 |
| 18. 모델의 과최적화를 피하는 방법 (overfitting, regularization) (8) | 2016.07.19 |
| 17. 여러개의 결과로 분류하는 방법 (multiclass classification:one vs all) (0) | 2016.07.18 |
| 16. Logistic Regression을 처리하는 방법 (5) | 2016.07.16 |



















댓글