37. 자율학습 두번째 (Principal Component Analysis) : PCA 적용하기

Reconstruction

지금까지 데이터를 압축하여 차원을 낮추는 방법에 대해서 알아보았습니다. 이번에는 다시 원래의 차원으로 복원을 하는 방법에 대해서 알아보도록 하겠습니다.(Reconstruction or Decompress) 이것은 원래의 데이터를 다시 찾기 위해서 사용되는 방법이 되겠습니다.

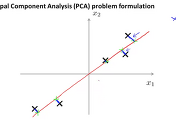
아래 그림에서와 같이 2차원 데이터들 x 를 직선에 투영하여 생성하였습니다. z = Ureduce T * X

다시 z 로 부터 X를 복원하기 위해서는 반대로 Ureduce * z = Xapprox 를 구하면 됩니다. 이때 Ureduce는 nxk의 크기를 갖는 matrix이고 z 는 kx1의 크기를 갖는 vector 이므로 Xapprox는 다시 n의 크기를 갖는 vector가 됩니다. 하지만 이렇게 복원을 한 n 차원의 데이터는 직선에 투영된 데이터가 되며 본래의 즉 투영 이전의 데이터와는 조금 다릅니다. 그렇기에 복원을 하여도 본래의 데이터에서 일부는 유실이 되게 됩니다.

이와 같은 방식으로 저차원의 압축된 데이터를 역으로 복원하여 원래의 고차원의 데이터로 다시 생성할 수 있게 되었습니다.

number of Principle Components

k 차원으로 낮추기 위한 방법들을 알아보았습니다. 이제 그럼 k 값은 어떻게 선택을 하는 것이 좋을지에 대해서 알아보겠습니다.

아래 그림에서와 같이 두가지 공식을 배웠습니다. 하나는 projection error 이고 또 하나는 원래의 데이터가 같는 전체적인 값입니다.

이 두가지를 비율로 나타내면 가운데 부분의 공식과 같이 됩니다.

이 값이 0.01 보다 같거나 작다고 생각해보겠습니다. 이것은 원래의 n차원의 데이터 x에 대하여 k차원으로 투영된 x approx의 차이를 의미하며 1%의 오차율이 있음을 알려줍니다. 이는 다시 이야기하면 99% 복원율을 나타내기도 합니다. 주로 많이 사용되는 비율이 1%, 5% 정도가 됩니다.

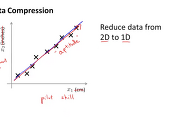
우리가 알고리즘을 구현하였으면 k 의 값이 1부터 커질 때의 이 비율 값을 비교할 수 있을 것입니다. 만약 아래그림의 예제와 같이 k 가 17의 값을 가질 때 이 비율이 1% 이하가 되었다면 우리는 k 를 17로 선택하여 사용하면 됩니다. 이렇게 k 를 선택하는 방법이 하나가 있습니다.

또 다른 하나의 방법은 svd(Sigma)까지 연산을 하고 이 결과로 나오는 S 값을 활용하는 것입니다. S matrix는 아래 그림의 오른쪽과 같이 대각선에 S11, S22, ... Snn 의 값을 가지는 matrix가 됩니다. 이 S 의 값을 Skk 까지 더하여 전체의 값과 비율로 나타낼 수도 있습니다. 아래 그림의 1 - sum 1-k (Sii) / sum 1-n (Sii) 의 값이 0.01보다 작거나 같은 k를 선택하는 것입니다. 

그리고 이것은 앞에 1 마이너스 부분을 빼면 복원률을 구할 수 있게 됩니다. 아래 그림의 하단 부분의 공식과 같이 0.99(99%) 의 값이 나오게 됩니다.

이것을 다시 정리하면 아래와 같이 공식이 됩니다. 이것을 이용해서 적절한 k 를 선택할 수 있게 되었습니다. 보통의 경우에 1000D을 100D 로 낮추는 경우가 가능하며 이러한 k 값을 잘 선택을 하면 원래의 데이터의 유실을 최소화 하면서 머신 러닝의 수행 성능에 큰 이점을 얻을 수 있어 유용하게 많이 사용이 되는 PCA 알고리즘입니다.

Advice for Applying PCA

PCA가 unsupervised learning 의 algorithm 이지만 머신러닝의 학습 시간을 단축할 수 있기에 supervised learning 에서도 활용이 가능합니다. 어떻게 적용이 되는지 알아보겠습니다.

아래 그림에서와 같이 x, y로 구성이 된 dataset에서 x features를 추출해 냅니다. 이때에는 y 의 결과값과의 매칭이 사라집니다.(unlabeled)

이렇게 추출된 x data가 10000D라고 하면 이것을 PCA를 통해서 1000D로 낮추고 이 때의 data를 z 라고 하겠습니다.

이렇게 새롭게 생성된 z data와 연관된 y data를 매칭하여 새로운 training dataset이 생성이 됩니다.

이때 h(x) 함수는 아래 그림의 오른쪽에 파란색 공식과 같이 x 대신 z로 표기된 sigmoid 함수로 변경됩니다.

여기서 x data를 z data로 mapping 하게 하는 것이 바로 U reduce Matrix가 되겠습니다. 복원시에도 사용이 되지요

이렇게하여 training set으로 생성된 새로운 맵핑 정보는 test set과 cv set에서도 사용이 가능합니다.

이러한 방식으로 차원을 낮추고 머신러닝의 학습속도를 높일 수 있으며 보편적으로 간단한 수준에서는 5~10배 정도의 차원을 낮추는것이 가능합니다.

이렇게 하여 PCA를 활용하여 메모리 사용율도 줄일 수 있고, 디스크 사용도 줄일 수 있게 됩니다. 또 머신이 학습하는 속도도 향상 시킬 수 있습니다. k 를 잘 선택하면 원래 데이터를 최대한 유지하면서 압축하는 것이 가능하게 되겠지요

또 그래프로 visualization 할때 자주 사용이 됩니다. 이때에는 그래프 상에 그리기 좋도록 k=2, 3 으로 만들어서 나타내게 됩니다.

하지만 PCA가 항상 좋은 것은 아닙니다.

원래의 데이터인 x를 z로 축소하여 사용하게 되기 때문에 fewer features에서 나타나는 overfit의 문제가 발생하게 될 수 있습니다. 또는 정상적인 머신러닝 시스템에서 overfit이 발생한다고 features를 낮추기 위해서 PCA를 사용하는 것도 그다지 좋은 방법이 되지 않습니다. 차라리 정규화의 lamdba 를 사용하는 것이 더 효과적으로 overfit을 다루기에 좋은 방법이 되겠습니다.

비록 PCA가 성능향상과 다양하게 사용이 될 수 있는 유용한 알고리즘이기는 하지만 모든 부분에 항상 사용하는 것은 좋치 않습니다. 그래서 또 한가지 추천하는 방식은 기본적으로 원래의 데이터인 x 를 이용하여 머신러닝을 수행해보고 만약에 디스크나 메모리 부족의 문제로 인하여 정상적인 수행이 어려운 경우이거나 혹은 너무 학습 시간이 오래 걸려서 문제가 되는 경우에만 PCA를 활용하여 사용하는 것이 더 나은 방법이 되겠습니다.