앞에서 수학적인 표현을 가지고 설명을 했던 내용을 다시 한번 NN 구성도를 보면서 살펴보도록 하겠습니다.
x, y의 dataset를 가지고 NN에 적용을 하게 되면 x data들은 input value의 형태로 Layer 1에서부터 시작이 됩니다. 이때 bias term인 상수 1은 존재하지만 크게 신경을 쓰지는 않습니다.
input values은 연결된 선들을 따라서 weight 값과 연산이 되어 layer2의 z라는 input values가 됩니다. 그리고 layer2의 unit(node)에서는 sigmoid 함수인 g의 함수로 연산이 되어 a(1)의 값을 가지게 되었습니다. 그리고 이 값은 다시 연결된 선을 따라가서 layer3의 input values가 될 것입니다.
z(3)1에 대하여 상세하게 보면 layer 2의 bias 값이 연결된 선을 따라 세타(2)10와 연산이 되어 input으로 옵니다. 이것을 수식으로 표현하면 아래 그림의 하단과 같이 나타낼 수 있습니다. [z(3)1 = 세타(2)10 * 1]
또 다른 input인 a(2)1도 연결된 선을 따라 세타(2)11와 연산이 되어 합쳐집니다. [z(3)1 = 세타(2)10 * 1 + 세타(2)11 * a(2)1]
마지막 input인 a(2)2도 연결된 선을 따라 세타(2)12와 연산이 되어 합이 됨으로서 최종적인 공식은 다음과 같이 됩니다.
z(3)1 = 세타(2)10 * 1 + 세타(2)11 * a(2)1 + 세타(2)12 * a(2)2
이렇게 연산이 되는 과정이 Forward Propagation입니다.
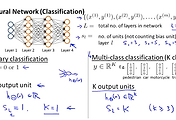
이번에는 dataset을 좀더 심플하게 하기 위해서 람다를 0으로 하여 정규화식을 제거하고 output 결과도 1개의 binary classification으로 하여 알아보겠습니다.
여기서 J 함수의 정규화식을 제외하고 나머지 부분중에서 내부에 있는 log로 이루어진 공식을 cost(i) 함수로 치환을 하겠습니다.
곧 J 함수는 cost(i)의 함수가 됩니다.
이제 Back Propagation에 대해서 알아보겠습니다.
델타(l)j는 l layer에 있는 j 번째 unit에 대한 cost error입니다. 이 델타(i)j를 구하기 위해서는 cost(i) 함수를 z(l)j 로 편미분하여 구하게 됩니다. cost(i) 함수는 위에서 치환한 log 로 구성되어 있는 함수이고 세타로 편미분을 하는 것에서 z 값으로 편미분을 하는 것으로 변경되었습니다. 이로 인해서 cost(i)의 함수내에 있는 h(x)함수가 조금 바뀌게 됩니다.
델타(4)1은 y(i) - a(i)1으로 최종 결과 값에 대한 예측된 결과 값의 차이가 되며 이것이 그냥 보면 cost와 비슷하지만 실제적으로는 error가 됩니다. 이것은 조금 다르다는 의미로서 바로 위에서 본것처럼 cost함수를 편미분하여 생성하는 값이기 때문입니다. 즉, z의 값으로 편미분을 했기 때문에 앞 layer의 input 값이 cost 함수에 미치는 영향을 분석하는 것이 되고 이것이 의미하는 것이 error가 됩니다.
델타(2)2를 상세하게 살펴보면,
Layer 2의 2번째 unit에서의 error는 연결된 선을 따라서 weight와 연산이 되어 다음 Layer 3의 두 unit에 영향을 줍니다. 그러므로 델타(2)2는 세타(2)12 * 델타(3)1 + 세타(2)22 * 델타(3)2의 값이 되는 겁니다.
같은 방식으로 델타(3)2는 녹색으로 연결된 결과 unit에 영향을 주게 되므로 델타(3)2의 값은 세타(3)12 * 델타(4)1이 됩니다.
이렇게 다시 한번 cost의 error를 의미하는 델타에 대해서 알아보았습니다.
이해하기가 쉽지는 않치만 중요한 내용이고 수년동안 많이 활용되어 온 알고리즘이라서 잘 알아두면 좋을 것 같습니다.
'Machine Learning' 카테고리의 다른 글
| 24. 뇌신경망을 이용한 머신러닝 (Neural Networks) 구성방안 (0) | 2016.07.25 |
|---|---|
| 23. 뇌신경망을 이용한 머신러닝 (Neural Networks) 구현하기 (0) | 2016.07.24 |
| 21. 뇌신경망을 이용한 머신러닝 (Neural Networks) Cost & BP (4) | 2016.07.22 |
| 20. 뇌신경망을 이용한 머신러닝 예제 (Neural Networks) (0) | 2016.07.21 |
| 19. 뇌신경망을 활용한 머신러닝 개념 (Neural Networks) (1) | 2016.07.20 |







댓글