최근 5년~10년 동안에 머신 러닝이 급격하게 발전한 이유중에 하나는 데이터가 많아졌기 때문이기도 합니다. 최근에 대두된 빅데이터의 시대가 보다 정확한 머신러닝에서의 학습에 큰 도움이 되기 때문입니다. 때문에 우리는 많은 데이터들을 통해 학습을 하게 되는 경우가 자주 발생합니다. 하지만 이런 빅데이터는 학습하는 속도에 영향을 미치기도 하며 알고리즘이 연산을 함에 있어서 연산 비용이 크게 증가하는 원인이 되기도 합니다.
이번에는 이렇게 스케일이 큰 데이터들을 다루는 방법(알고리즘)들에 대해서 알아보도록 하겠습니다.
우리가 이전에도 살펴보았듯이 머신 러닝에서 어느 알고리즘을 사용하면 더 좋은 성능을 보이는가에서는 크게 차이가 없었습니다. 하지만 데이터의 사이즈가 커질 수록 더 좋은 결과가 나타난다는 것은 명확하게 알고 있습니다.
우리가 머신 러닝을 접하면서 일반적으로 dataset의 수인 m 이 100,000,000 인 경우가 많이 발생합니다. 예를 들어, 인구조사를 한다거나 웹사이트의 트래픽 데이터를 활용하는 경우에 쉽게 1억건 이상의 데이터가 발생하지요
이런 빅사이즈의 시스템에서는 어떻게 학습을 시키는 것이 좋을까요?
아래 그림에서와 같이 세타를 학습하기 위해서 편미분된 공식을 이용해서 gradient descent algorithm을 수행한다고 생각해보겠습니다. 1억건의 dataset에 대해서 연산을 해야하기에 한번 세타를 업데이트 할 때마다 1억건의 데이터들을 더하는 연산이 수행이 될 것입니다. 오늘날에 CPU 나 GPU의 사양이 좋아졌음에도 불구하고 이런 연산은 많은 비용과 시간을 사용하게 될 것입니다.
이런 경우 보다 효율적으로 학습을 하기 위한 방법중에 하나가 1억건 대신에 약 1천건만 먼저 training을 하는 것입니다. 랜덤하게 선택된 데이터 1000건을 선별하고 이것을 training set으로 하여 먼저 학습을 시켜본 이후에 아래 그림에서와 같이 training size에 대한 error를 그래프로 그려보는 것입니다.
만약 왼쪽 그래프와 같이 보여진다면 이 시스템은 high variance problem 을 가지고 있는 것입니다. 또 오른쪽 그래프와 같이 보여진다면 high bias problem 인 것이지요. 이처럼 처음부터 모든 1억건의 데이터를 돌려보는 것보다 훨씬 효과적으로 시스템(혹은 알고리즘)을 진단하고 그에 적절하게 features를 추가해본다거나 NN의 경우에는 hidden units을 추가해보는 것으로 조절을 할 수 있을 것입니다.
Stochastic gradient descent
Linear regression에서의 gradient descent algorithm을 다시 떠올려보겠습니다.
아래 그림과 같이 h(x)와 J train 공식이 있고 이것을 세타 parameter에 대해서 편미분하여 업데이트 하도록 하였습니다. 이때 J 함수를 그래프로 표현하면 오른쪽과 같이 활 모양으로 생긴 함수였습니다. 우리의 목적은 이 함수에 대한 global minimum을 찾는 것이였지요
gradient descent가 수행이 되면서 연산하여 업데이트를 하는 과정을 빨간색 점으로 그래프 상에 표현을 하면 아래 그림과 같이 됩니다. 점차적으로 중심점을 찾아 한발씩 이동하게 됩니다. 이러한 방식의 알고리즘을 또 다른 식으로 표현을 하면 batch gradient descent 라고 합니다. 한번 전체적으로 연산하고 한번 이동하게 되지요.
만약에 연산해야 하는 dataset이 3억건이라고 하면 어마어마한 연산과 시간이 필요하게 될 뿐만아니라 많은 공간의 메모리를 사용해야 하고 수많은 디스크 I/O가 발생하면서 시스템에 부하를 주게 될 것입니다. 그래서 이보다 더 효율적인 알고리즘이 필요하게 된 것입니다.
이와 같은 문제를 효과적으로 하기 위해서 나온 알고리즘이 바로 Stochastic gradient descent 입니다.
공식도 조금 다릅니다. 아래 오른쪽의 J train 함수를 두개의 공식으로 분리하여 만듭니다. summation 안쪽에 squared error 부분을 별도로 cost 함수로 놓습니다. 이때 cost 함수는 x, y가 하나인 공식이 됩니다. 즉 한개의 data row에 대한 값이 됩니다.
이렇게 연산된 cost 값들을 최종적으로 모든 dataset에 대해서 summation을 하여 J train 을 만듭니다.
이렇게 실제적으로 동일한 J 함수이지만 동작하는 것이 조금 다르게 됩니다. 먼저 training data들을 랜덤하게 섞어(shuffle or reorder) 줍니다. 그리고나서 세타에 대한 편미분을 반복적으로 수행을 하는데, 이때 cost( 세타,x,y )에 대해서 편미분을 해줍니다. summation이 없습니다.
이렇게 하므로서 전체 데이터셋을 모두 연산하지 않고 하나의 데이터(row)씩 순차적으로 연산하고 업데이트 반영하게 되었습니다.
이와 같은 움직임을 그래프상에 표현을 하면 아래와 같이 됩니다.
첫번째 data를 연산하여 방향을 잡고 이동합니다. 운이 좋으면 global minimum 쪽으로 올바른 방향을 잡고 이동하게 됩니다. 그리고 두번째 data를 연산하였는데 조금 방향이 틀어져서 이동을 했습니다. 그래도 크게 문제가 되지 않습니다. 그 다음 3번째, 4번째.... m 만큼 이동을 하게 되면 한번에 바로 가지는 못하지만 돌고 돌아서 이동하게 될 것입니다.
이렇게 이동하여 결국 전반적으로는 global minimum쪽으로 이동을 하게 됩니다. 뭐 정확히 중심점을 찾기는 어렵겠지만 그 근처 어딘가쯤으로 도착을 하게 될 것입니다. 하지만 이것은 크게 문제가 되지 않습니다. 중심점의 근처만 찾더라도 결과가 크게 차이가 나지 않을 것이고 또한 batch 방식보다 더 빠르게 찾게 될 것이기 때문입니다.
실제로 이 알고리즘을 구현할때에는 for구문의 반복 횟수를 전체 dataset 보다 1배에서 10배 사이로 해주는 것이 좋습니다. 우리가 정말로 큰 빅데이터를 가지고 있다면 이러한 방법으로도 충분히 훌륭한 hypothesis를 가지게 될 것이기 때문입니다. 그리고 이렇게 하여 전체 빅데이터에서 global minimum을 찾아가기 위한 K passes가 존재하게 되며 이때의 K 는 목표까지 가기위하여 반복적으로 수행하는 step의 수를 의미합니다.
Mini-batch gradient descent
이번에 배울 mini-batch 는 batch와 stochasitc의 중간단계와 같이 수행이 됩니다. batch의 경우에는 각각의 iteration(반복처리시) 마다 모든 dataset인 m 개의 data들을 연산하는 것이고 stochastic의 경우에는 각각의 iteration 마다 1개의 data만 연산을 하는 것입니다. 이번에 배울 mini-batch는 각각의 iteration 마다 예를들어 10개의 data 씩으로 연산을 묶어서 하도록 하는 방식이 되겠습니다. (b=10)
한번 연산을 수행할때 10개씩 연산을 하기 때문에 당연히 batch 보다 속도가 빠르며 또 때로는 stochastic 보다도 빠른 속도를 낼 수 있기도 합니다.
공식은 아래 그림과 같습니다. b가 10일때 반복문인 for구문에서는 1, 11, 21... 로 10개씩 뛰면서 돌게 되고 각 iteration 에서는 for 구문 내의 공식과 같이 k=1 부터 i+9까지 10개의 데이터에 대해서 연산을 하도록 합니다. 이 방식이 stochastic 보다 빠르게 되는 이유는 10개 연산시에 vectorization 을 사용하게 되면 한번 연산에 10개 연산을 할 수 있도록 되어 부분적으로 병렬적인 연산이 가능하게 되기 때문입니다.
일반적으로 b의 갯수를 10을 주로 사용하지만 특별하게 dataset에 맞추어 최적값을 찾아서 사용해도 좋습니다. 참고로 만약에 b가 1이 되면 stochastic과 동일하게 동작을 하게 될 것이고, 또는 b 가 m 과 같게 주어지면 batch 와 동일하게 수행이 되게 됩니다.
Stochastic gradient descent convergence
Stochastic gradient descent 알고리즘을 사용할때 global minimum으로 수렴을 잘 하고 있는지를 디버깅하는 방법과 Learning rate alpha를 어떻게 조절하는지에 대해서 알아보겠습니다.
기존에 batch 방식에서는 매 iteration 마다 gradient descent가 cost 값을 줄여 나가는 것을 볼 수 있었습니다. 적은 데이터를 사용할 경우에는 이것이 좋치만 빅데이터를 사용할 경우에는 사용할 수가 없는 단점이 있었죠
반면에 stochastic 방식에서는 한개의 데이터씩 연산을 하므로서 전체 데이터를 연산하다가 시스템이 뻣는 경우가 생기지 않습니다. 하지만 한건씩 연산을 하기 때문에 매 iteration 마다 정확한 경로를 찾아가지 못하고 살짝 경로를 돌아서 가기 때문에 1000 iteration에 한번씩 로깅을 해보는 것이 좋습니다. 1000건 처리하고 그때의 cost 결과를 그래프상에 표현을 해보면 잘 수행이 되고 있는지 cost가 감소하고 있는지를 확인할 수 있게 됩니다.
cost( 세타,x,y ) 가 1000번 수행할 때마다의 결과를 그래프로 나타내면 아래 그림과 같이 됩니다. 먼저 왼쪽 상단의 그래프를 보겠습니다. 1000번씩 로깅한 그래프가 파란색으로 그려진 그래프입니다. 약간의 진동(노이즈)이 있어 보이지만 cost가 감소하다가 일정 시점이 지나면서 수렴하는 것같아 보입니다. 만약에 learning rate의 알파값을 더 작은 값으로 설정을 하고 다시 기록을 하게 되면 빨간색과 같은 그래프를 보이게 됩니다. 이는 알파값이 작아졌기 때문에 하강하는 스탭사이즈가 작아짐으로서 천천히 하강을 하게 됩니다. 하지만 후반으로 갈수록 더 잘 수렴하는 것을 볼 수 있습니다.
두번째 그래프는 첫번째 그래프보다 더 잘 감소를 하고 있어 좋은 성능과 결과를 보여주고 있습니다. 1000번씩 로깅한 파란색 선은 진동(노이즈)이 보입니다. 그리고 5000번에 한번씩 로깅을 하게 되면 빨간색 선과 같이 됩니다. 좀더 부드럽게 보여지고 역시 감소하고 있으니 잘 수렵이 되고 있다고 볼 수 있겠습니다. 5000번 마다 로깅한 빨간색 선은 1000번 마다 로깅한 파란색 선보다 부드럽게 나타납니다. 하지만 빨간색의 선이 항상 좋은 것은 아닙니다. 왜냐하면 로깅이 1000번씩 했을때는 5번 피드백이 발생하는데 비해서 1번 피드백이 발생하기 때문에 모니터링이 느리게 될 수 있습니다.
세번째 그래프는 1000번씩 로깅한 파란색 선은 진동이 크고 수렴한다고 보기 어렵습니다. 이와 같이 나타나는 경우에는 데이터셋에 노이즈가 많아서 일수 있으므로 로깅 사이즈를 늘려주는 것이 좋습니다. 5000번씩 로깅한 빨간색 선으로 보면 보다 덜 노이지하게 수렴해 가고 있는것을 볼 수 있기 때문입니다. 이것은 결론적으로는 성과가 그리 좋치 않은 알고리즘 같네요. 이런 경우에는 feature들을 변경해주거나 learning rate를 조절해주는 것이 필요할 것 같습니다.
네번째 마지막 그래프를 보면 감소하는 것이 아니라 상승하고 있습니다. convergence가 되어야 하는데 divergence가 되고 있는 모습니다. 뭔가 알고리즘에 문제가 있는 것처럼 보이네요. 이런 경우에는 learning rate을 작게 하는 것이 좋습니다.
이와 같이 cost의 그래프를 보면 학습을 하는 과정에서 발생하는 문제점들을 모니터링 할 수 있습니다. 대표적으로 너무 노이지하게 그래프가 나타날 때에는 로깅하는 데이터사이즈를 늘려주면 보다 부드럽게 하강하는 것을 볼 수 있게 됩니다. 혹은 수렴을 하지 않거나 발산을 하는 경우에는 learning rate를 줄여주면 더 잘 수렴하게 됩니다.
그러면 Learning rate alpha를 어떻게 조절하는 것이 좋을까요?
대부분의 위의 경우에서는 alpha를 고정된 상수 값으로 사용하였습니다. 그런데 minimum을 찾아서 converge가 되길 원한다면 시간이 지날수록, 연산이 계속 수행이 되면서 일정시점에 수렴하는 듯하게 될때에 alpha도 자연스럽게 감소하게 되는 것이 좋습니다.
그렇게 하기 위해서 alpha 값을 다음과 같이 연산하도록 하면 됩니다. 분자와 분모에 상수를 사용하되 분모에 iterationNumber를 추가하여 반복 연산이 진행이 될 수록 전체 값이 작아지도록 만드는 것입니다.
α = const1/(iterationNumber + const2)
고정된 alpha를 사용했을때는 외쪽의 그림과 같이 minimum 근처에서 수렴하지 못하고 돌게 되는 것에 반면에, 위와 같이 alpha값이 점차적으로 줄어들게 하면 오른쪽 그림과 같이 minimum에 안정적으로 안착하게 되는 것을 볼 수 있습니다.
'Machine Learning' 카테고리의 다른 글
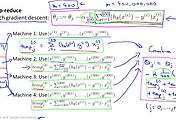
| 46. 빅데이터 대응하기 : 분산환경 처리하기 (Map Reduce & data parallelism) (0) | 2016.09.07 |
|---|---|
| 45. 빅데이터 대응하기 : 스트림형 데이터 처리하기 (Online learning) (1) | 2016.09.06 |
| 43. 추천 시스템 : 관련된 다른 상품을 추천해주기(Low Rank Matrix Factorization) (0) | 2016.09.04 |
| 42. 추천 시스템 : 유저와 머신러닝이 함께 만들기(Collaborative Filtering Algorithm) (0) | 2016.09.03 |
| 41. 추천 시스템 : Recommender Systems 개요 (0) | 2016.08.30 |














댓글