이전내용과 이어서 이번에는 Collaborative Filtering 이라 불리우는 알고리즘에 대해서 알아보겠습니다.
이 알고리즘은 학습을 통해서 어떤 feature가 의미가 있는지를 배울 수 있습니다.
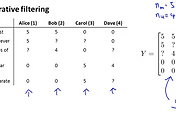
이전 내용에서 다루었던 예제를 다시 살펴보겠습니다. 아래 그림과 같이 5개의 영화와 4명의 유저가 평점을 기록합니다. 우리는 x1, x2의 x feature가 어떤 내용인지 알지 못합니다. 이전에서는 x feature를 알고 유저의 선호도(세타)를 찾는 방식이였던 것과 대조적이네요
유저가 남긴 평점을 토대로 하여 각 유저의 선호도인 세타를 아래 그림의 하단과 같이 나타내보았습니다. Love at last란 영화가 어떤 특징을 가지는 지는 모르겠지만 Alice와 Bob은 5점을 주어 선호도가 높음을 알 수 있습니다. 때문에 세타(1)은 [5; 0] 이 됩니다. 첫번째 parameter가 뭔지는 모르지만 선호도가 높은것이죠. 여기에 bias term을 추가해주어 세타(1)은 [0; 5; 0]이 됩니다. 마찬가지로 bob의 선호도인 세타(2)도 같습니다.
그리고 Carol과 Dave를 보니 Alice와 Bob과는 반대로 평점을 주고 있음을 알수 있습니다. 반대되는 선호도를 가지고 있기에 세타(3)와 세타(4)는 [0; 0; 5]라고 할 수 있겠습니다.
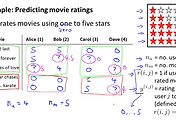
이렇게하여 선호도를 알게 되었습니다. 이제 선호도와 x feature 를 곱하면 평점을 예상할 수 있으니 공식에 대입해서 풀어보면 다음과 같이 될 것입니다. 세타(1)T * X(1) = 5, 세타(1)이 [0; 5; 0] 임으로 x(1)은 [1; 1.0; 0.0] 이 되면 결과값이 5가 되어 앞에 공식을 만족하게 되겠지요
이와 같은 방식으로 선호도를 통해서 x feature를 알아 낼 수 있고 이를 이용하여 평점이 아직 없는 ? 부분에 대해서 유저들마다의 예상 평점도 예측할 수 있을 것입니다.
하나의 영화에 대한 x features 인 x(i)를 학습하기 위한 공식을 보면 아래 그림의 상단과 같이 됩니다. 각 유저들의 선호도(세타)들이 주어지면 이를 통해서 x(i) features를 학습을 통해서 찾아낼 수 있습니다. 뒤에는 x(i)에 대한 regulazation term이 되고 당연하겠지만 bias term을 제외하고 1부터 시작합니다.
이를 모든 영화에 대해서로 확장을 해보면 밑에쪽 공식과 같이 각 영화들에 대한 합으로 summation이 추가됩니다. 이것이 우리의 J 함수가 되겠습니다.
이전 내용에서 배웠던 알고리즘은 x features(영화에 대한 장르정보)가 주어졌을때 유저들의 선호도(세타)를 찾는 내용이었고, 이번에 배운 내용은 반대로 유저들의 선호도가 주어졌을때 x features를 찾는 내용이 됩니다. 이것은 닭이 먼저냐 달걀이 먼저냐 하는 문제와 비슷하게 동일한 내용을 두고 다르게 접근 하는 방식이 됩니다.
실제적으로 이 두가지 알고리즘을 혼합해서 사용하면 상당히 괜찮은 알고리즘이 되고 그로 인해서 훌륭한 결과를 낼 수 있게 됩니다. 이를 혼합하는 방식은 반복적으로 번갈아 가면서 수행하도록 하는 것입니다. 먼저 랜덤한 값으로 초기 셋팅을 한 세타를 통해서 x features를 찾아내고, 이 x features를 통해서 다시 선호도를 예측하고 실제 결과와 비교하여 최적화 시켜나가는 것입니다. 그리고 이 프로세스를 계속 반복적으로 수행하게 되면 자동으로 x features를 찾음과 동시에 유저의 선호도도 정확하게 예측할 수 있게 되는 것이 원리입니다.
이렇게 유저가 활동을 통해서 (평점을 주는 행위) 알고리즘이 학습할 수 있도록 도움을 주기 때문에 의미가 있으며 이러한 알고리즘을 Collaborative Filtering Algorithm이라 합니다.
Optimization Objective
Collaborative filtering algorithm을 구성하기 전에 위에서 배운 두가지 개념을 어떻게 하나로 합치는지에 대하여 알아보겠습니다.
아래 그림의 첫번째 공식은 features x가 주어졌을때 유저들의 선호도인 세타를 찾는 공식이였습니다.
그다음 두번째 공식은 유저들의 선호도(평점) 세타가 주어졌을때 영화에 대한 features x를 찾아내는 공식입니다.
위에서 살펴본 이 두가지를 혼용하는 방식은 초기 parameters의 값을 랜덤으로 주고 두가지 공식을 번갈아가면서 반복적으로 수행하는 것이였습니다. 그런데 그보다 더 효율적인 방법으로 두가지 공식을 합칠 수 있습니다. 바로 마지막의 공식과 같이 features x 와 세타에 대해서 동시적으로 풀어내는 것입니다.
좀더 상세하게 살펴보겠습니다.
잘보면 첫번째 공식의 squared error term (분홍색 박스) 과 두번째 공식의 것이 거의 비슷합니다. 다만 다른점은 summation 할 때 유저 j에 대해서 r(i,j)=1 인것만 더할 것인지, 영화 i에 대해서 r(i,j)=1 인것만 더할 것인지가 다릅니다. 이것을 하나로 합치면 모든 i와 j에 대해서 r(i,j)=1 인것을 sum하면 될것입니다.
그리고 뒷부분의 Regularization terms (빨간색박스, 하늘색박스) 은 그대로 뒤에 추가해주면 됩니다.
이렇게 생성된 혼합된 새로운 공식은 x와 세타에 대해 동시에 학습을 하도록 할 수 있습니다. 그리고 이전 공식에서는 x0=1의 bias term을 고려하였으나 새로운 공식에서는 이것을 고려할 필요가 없습니다. 때문에 x와 세타는 모두 n-dimensional vector가 됩니다. (n+1이 아닙니다.)
이렇게 되는 이유는 이 알고리즘이 새로운 feature가 필요하다면 하나를 자동으로 생성하고 그 feature의 값을 1로 생성을 하기 때문에 우리가 직접 feature를 생성하고 값을 줄 필요가 없기 때문입니다.
이제 완성된 Collaborative filtering algorithm을 정리해보면 다음과 같습니다.
1) x 와 세타의 초기값을 작은 랜덤 값으로 줍니다. (NN에서 했던것과 비슷합니다.)
2) Gadient descent 혹은 advanced optiimization 알고리즘을 사용해서 minimize를 합니다. 모든 x, 세타의 parameter에 대해서 편미분한 공식을 사용하여 업데이트를 해나갑니다. 이때 x0, 세타0가 없으니 이에 대해 고려하지 않고 모든 parameter에 대해서 regularization term을 적용하면 됩니다.
3) 이렇게 학습하여 찾아낸 x features와 세타 parameters를 곱하여 유저가 영화에 대한 평점을 예측할 수 있게 되었습니다.
'Machine Learning' 카테고리의 다른 글
| 44. 빅데이터 대응하기 : Large Scale Machine Learning (5) | 2016.09.05 |
|---|---|
| 43. 추천 시스템 : 관련된 다른 상품을 추천해주기(Low Rank Matrix Factorization) (0) | 2016.09.04 |
| 41. 추천 시스템 : Recommender Systems 개요 (0) | 2016.08.30 |
| 40. 이상(사기) 탐지 : 또 다른 탐지 알고리즘 (Multivariate Gaussian Distribution) (6) | 2016.08.29 |
| 39. 이상(사기) 탐지 : Anomaly Detection System 만들기 (0) | 2016.08.28 |








댓글