추천 시스템은 오늘날에 가장 많이 사용되는 알고리즘입니다. 다양한 분야의 서비스에서 사용되고 있으며 대표적으로는 아마존과 같은 쇼핑 사이트에서 추천상품이나 iTunes의 genius 서비스에서 사용되고 있습니다.
특히 아마존에서는 이러한 추천 서비스가 매출에 큰 영향을 미치고 있습니다. 이 추천 서비스를 개선하는 것이 직접적인 수입에 기여를 하는 방법이기도 합니다.
재미있는 것은 추천서비스는 학문적으로는 크게 주목을 받지 않을 만큼 기술적인 특색이 없지만, 상업적으로는 아주 중요한 서비스로 인식이 되고 있다는 것입니다. 사실상 기술적으로는 큰 이슈가 없지만 아이디어의 차이가 추천 서비스의 핵심이라고 할 수 있습니다. 어떤 features를 사용하느냐에 따라서 추천 서비스가 달라지며 핵심 features들을 찾는 것이 관건이 됩니다.
아래 예제와 같이 영화에 대한 평점 서비스를 한다고 생각해보겠습니다.
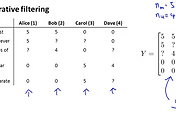
5개의 영화가 있고 4명의 사람들이 각각의 영화에 대해서 1~5개의 별점을 줄 수 있습니다. 아래 표와 같이 어떤 사람은 5점을 주고 다른 사람은 0점을 주기도 하며, ? 는 해당 영화에 대해서 평점을 주지 않는 사람을 의미합니다.
유저수를 nu , 영화의 수를 nm , 유저 j 가 영화 i 에 대해서 평점을 주었다면 r(i, j) =1 이 되며, 이때 유저 j 가 영화 i 에 부여한 별점을 y(i,j) 라고 하겠습니다.
아래 데이터를 분석해보면 Alice와 Bob은 위에 3개 영화(로맨틱)에 대해서 높은 점수를 주었으며, 아래 2개의 영화(액션)에 대해서는 0점을 주었습니다. 이로서 둘은 로맨틱 영화를 선호하고 액션 영화를 좋아하지 않는 것을 알수 있습니다. 반면에 Carol과 Dave는 로맨틱 영화들에게는 0점을 주었고 액션 영화에 대해서는 높은 별점을 주었습니다. 이로서 이 둘은 액션 영화를 선호하는 것을 알수 있습니다.
이를 이용해서 중간에 있는 ? 표시의 missing values는 학습 알고리즘을 통해서 채워줄수도 있을 것입니다.
Content based recommendation
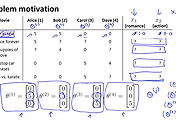
위 예제에서 영화의 장르 정보를 feature로 생성하면 x1(로맨스), x2(액션)가 됩니다. 그리고 각각의 영화는 이러한 feature vector를 가지고 있다고 할 수 있습니다. 또 x feature는 상수값인 x0 = 1 (bias term) 의 값을 가지고 있습니다.
첫번째 영화인 Love at last의 경우를 보면 x(1)은 [1; 0.9; 0] 의 값을 갖는 feature vector로 표현이 됩니다. 이렇게 x1 부터 x5까지의 dataset이 아래 그림의 오른쪽 값들로 만들어지게 되겠습니다.
그리고 각 유저에 대한 parameter를 세타로 놓으면, 이 세타는 유저의 성향도를 나타내는 vector가 됩니다. 즉, 세타와 x 의 곱이 별점이 되는 공식이 생성됩니다. 아래 예제에서 Alice의 성향인 세타(1)은 [0; 5; 0;]의 값을 갖는 parameter vector가 될 것입니다. 이제 Alice가 아직 평점을 주지 않은 3번째 영화에 대한 ? 를 예측해 볼 수도 있습니다. ( (θ1)T * x3 = (0 * 1) + (5 * 0.99) + (0 * 0) = 4.95 )
이와 같이 영화의 장르와 유저의 성향도를 통해서 적절하게 예측을 할 수 있음을 알아보았습니다
지금까지 다룬 각각의 변수들과 의미를 정리하면 아래 그림과 같습니다. 여기서 중요한 것은 유저가 평점을 남겼다는 정보인 r(i,j)가 1인 정보입니다. 이 정보를 통해서 유저가 실제적으로 영화에 대해 평가를 한 별점만을 선별할 수 있으므로 보다 정확한 평가가 가능해질 것입니다. 다시 말하면 의미 있게 사용할 수 있는 정보를 식별할 수 있게 되는 것이지요
그리고 아래 m(j)는 유저 j가 별점을 부여한 영화들의 수입니다. 아래 공식에서 분모에 있는 m(j)는 무시하여도 minimize 하는데 큰 지장이 없음을 이전에 배웠으니 아래 공식에서 빨간색 엑스표로 삭제하였습니다
이렇게 생성된 parameters과 공식들로 머신이 학습을 통해 세타를 찾는 과정은 이전에 linear regression과 비슷합니다. 그리하여 아래 그림 하단의 공식을 minimize하는 것이 우리의 목표가 되겠습니다.
이제 공식을 조금더 살펴보겠습니다.
유저 j에 대한 parameter인 세타(j)는 의미적으로는 유저가 영화에 대한 선호도가 됩니다. 그렇기 때문에 세타(j)T x(i)는 i 영화에 대한 유저 j가 주는 평점(별점)을 예측하는 값이 됩니다. 이것을 y(i,j)와 비교하면 실제 값과의 차이 즉, error 값이 되겠습니다. 그리고 이것은 유저 j가 평가를 한 영화 i 에 대해서만 수행을 합니다.(i:r(i,j)=1)
그리고 뒷부분은 많이 보던 regularization term(정규화식)이 lambda와 세타로 구성이 되어 있고 k가 1부터 n까지의 합이 됩니다. (bias term인 x0=1 을 제외했던 것 기억나시죠?)
이렇게 한명의 유저 j에 대한 세타(j)에 대한 공식이 되었습니다. 이제 다수의 유저에 대한(nu) 식으로 확장을 하면 아래 그림의 하단의 공식과 같이 됩니다. j가 1부터 nu 까지의 합이 추가되었지요
이렇게 탄생한 모든 유저들에 대한 세타들의 함수가 바로 J 함수(cost function)이 되었습니다.
이제 이 J 함수를 각각의 parameter에 대해서 편미분하여 동시에 업데이트가 되도록 구현하면 학습을 할 수 있는 Gradient descent algorithm을 사용할 수 있게 되겠습니다. Gradient descent 외에도 Advanced Optimization Algorithms을 사용해도 됩니다.
그리고 이전에 배운것처럼 regularization은 k가 1부터만 적용을 해주면 되겠습니다.
linear regression과 거의 비슷하지요? 차이점이라고 하면 공식에서 1/m 만 없다는 것일 겁니다.
지금까지 배운 방식은 영화(content)라는 컨텐츠를 기준으로 또는 영화가 가지고 있는 features을 통해서 유저들에게 어떠한 영향을 주고 있는지를 알아보는 방법이라고 할 수 있습니다. 이러한 접근 방식을 Content based recommendation 라고 합니다. 그리고 이것은 features를 직접 만들어주어야 한다는 것이 조금 애매할 수 있습니다. 다음 내용은 보다 널리 이용되는 추천 알고리즘에 대해서 알아보겠습니다.
'Machine Learning' 카테고리의 다른 글
| 43. 추천 시스템 : 관련된 다른 상품을 추천해주기(Low Rank Matrix Factorization) (0) | 2016.09.04 |
|---|---|
| 42. 추천 시스템 : 유저와 머신러닝이 함께 만들기(Collaborative Filtering Algorithm) (0) | 2016.09.03 |
| 40. 이상(사기) 탐지 : 또 다른 탐지 알고리즘 (Multivariate Gaussian Distribution) (6) | 2016.08.29 |
| 39. 이상(사기) 탐지 : Anomaly Detection System 만들기 (0) | 2016.08.28 |
| 38. 이상(사기) 탐지 : Anomaly Detection System 개요 (4) | 2016.08.24 |







댓글