이번에는 collaborative filtering algorithm에서 한단계 더 나아가서 어떤 손님이 영화를 보고자 할때 관련된 다른 영화들을 추천해주는 방법에 대해서 알아보도록 하겠습니다.
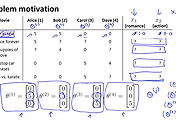
이전에 배운 예제를 다시 가져오면 아래 그림과 같습니다. 5개의 영화가 있고 4명의 유저가 있습니다. 이들이 준 평점들은 Y로 나타낼 수 있습니다.
Y가 주어졌기 때문에 이것을 x 와 세타로 표현하면 아래 그림의 오른쪽 matrix와 같이 됩니다.
Y = 세타T(j) * x(i)
여기에서 모든 영화가 가지고 있는 x features들을 하나의 row로 합쳐서 X vector를 만들면 아래 그림 왼쪽 밑에와 같이 됩니다.
또, 모든 사람이 가지고 있는 선호도인 세타 parameters들을 하나의 row로 합쳐서 θ vector도 만들 수 있습니다.
이렇게 X와 θ가 주어지면 우리는 X * θT 와 같은 벡터 연산을 통해서 결과를 예측할 수 있게 되었습니다. 이러한 방식의 알고리즘을 Low Rank Matrix Factorization 라고 합니다. 바로 X 와 θ가 low rank matrix가 되며 이둘을 linear algebra(선형대수학)으로 풀어낼 수 있기 때문입니다.
그럼 다른 영화를 관련된 영화로 추천하는 방법을 알아보겠습니다.
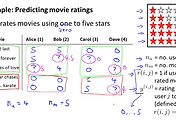
우리는 이전에 배운 collaborative filtering algorithm을 통해서 각각의 영화 i 가 가지고 있는 feature vector x를 찾아냈습니다. 아마도 찾아낸 feature가 무엇인지 우리가 알기에는 어려울 수 있습니다. 하지만 각각의 feature가 로맨스, 액션, 코메디라고 해보겠습니다. (실제적으로는 이 feature들이 어떤 것인지 정확하게 사람이 인지하기 어려울 수도 있습니다. 이것은 유저들이 좋아하는 영화에 대한 특징, 즉 의미가 있어 보이는 정보들을 머신이 이해하기 위해서 만들어지는 것이기 때문입니다.)
이제 영화 i 와 관련된 영화인 j를 어떻게 하면 찾을 수 있을까요?
이것은 두가지 영화가 얼마나 비슷한가를 의미하기도 합니다. 비슷한 영화를 찾기 위해서 좋은 방법은 우리가 알고 있는 영화의 특징이 되는 features를 활용하는 것입니다. 수학적으로는 두 영화 사이의 거리를 측정하여 가장 가까운 거리를 갖는 영화를 추천하면 되는 것이지요
minimize ||xi - xj||
그리고 이것은 실제 영화가 가지고 있는 특징이라고 하기 보다는, 유저들이 좋아하는, 유저 입장에서 바라봤을때의 영화가 가지고 있는 특징요소에 대한 비교라고 할 수 있겠습니다.
자 이제 마지막으로 한가지만 더 살펴보겠습니다. 만약에 새로운 유저가 영입이 되었다고 생각해보겠습니다. 이 다섯번째 유저(Eve)는 아직 영화에 대한 평점을 하나도 남기지 않은 상태입니다. 이런 경우에 어떤 문제가 발생하는지 생각해보겠습니다.
아래의 공식이 있습니다. Eve 유저는 평점을 남긴 영화가 없기 때문에 r(i,j)가 모두 0이 됩니다. 즉, 공식 앞부분의 squared error term이 의미가 없게 되는 것이지요. 그럼 남은것은 뒤에 regularization terms 입니다. 그런데 이 term을 minimize 하면 당연히 세타는 0으로 가게 되겠지요. 그리하여 세타 vector는 [0; 0]이 될 것입니다. 결국 세타T * x도 0이 되므로 모든 영화에 대한 평점이 0점으로 주어지게 되는 결과가 나타납니다.
이렇게 되면 이 신규 유저에 대해서는 다른 영화를 추천할 수 없게 되는 문제가 생기게 됩니다.
이것을 해결하고자 사용되는 방법이 Mean Normalization 입니다.
쉽게 이야기하면 영화에 대한 유저들의 평점 평균을 이용해서 신규유저에게 주어지게 되는 것입니다.
아래 그림과 같이 Y 값들이 있습니다. 4명이 평점을 주었으니 이들 값에 대한 평균치를 계산하면 바로 오른쪽에 μ vector의 값이 됩니다. 이 값을 이용해서 Y를 다시 재정의를 해보면 맨 오른쪽의 Y matrix가 됩니다. 평균치 값에 실제 유저가 평점한 내용의 값을 + 혹은 -로 0을 기준으로 차이를 두어 만든 것입니다.
이것을 수학적 공식으로 만들면 중간쯤에 있는 공식과 같이 됩니다. (θ5)T xi + μi
이때도 마찬가지로 세타가 0의 vector임으로 자연스럽게 영화들의 평균 값인 μ만 남게 되고 신규 유저들과 같이 아무런 평점이 없는 유저에게는 이 값이 적용이 되어지게 될 것입니다.
이렇게 하면 신규 유저들에게도 다른 영화를 추천할 수 있게 되어집니다. 이 방법이 우리가 사실상 사용할 수 있는 가장 좋은 방법입니다. 아예 아무것도 추천하지 못하는 것보다는 나으니까요
한가지 참고로 위의 예제에서는 features scaling을 사용하지 않았습니다. 왜냐하면 영화의 평점이 모두 1~5로 정해져 있어 비슷한 값들을 가지고 있기 때문이였습니다. 만약 다른 분야에 적용할 때에는 이를 고려해서 알고리즘을 사용하여야 합니다.
여러분은 지금까지 추천 알고리즘에 대해서 전반적인 내용들을 모두 배우셨습니다.
'Machine Learning' 카테고리의 다른 글
| 45. 빅데이터 대응하기 : 스트림형 데이터 처리하기 (Online learning) (1) | 2016.09.06 |
|---|---|
| 44. 빅데이터 대응하기 : Large Scale Machine Learning (5) | 2016.09.05 |
| 42. 추천 시스템 : 유저와 머신러닝이 함께 만들기(Collaborative Filtering Algorithm) (0) | 2016.09.03 |
| 41. 추천 시스템 : Recommender Systems 개요 (0) | 2016.08.30 |
| 40. 이상(사기) 탐지 : 또 다른 탐지 알고리즘 (Multivariate Gaussian Distribution) (6) | 2016.08.29 |







댓글