SVM의 강점인 Large Margin에 대해서 벡터를 이용해서 한번 원리를 이해해보도록 하겠습니다. 어떤 원리로 margin이 생기는지를 알면 더 효율적으로 알고리즘을 사용할 수 있을 것 같습니다.
아래 그림과 같이 두개의 벡터 u, v가 있습니다. 각각 2개의 값을 가지고 있고 이 두개의 벡터의 곱에 대해서 생각해보겠습니다. 각각의 벡터를 그래프 상에 표현을 하면 아래 왼쪽과 같이 됩니다. u 벡터는 파란색의 u1, u2의 좌표를 갖는 원점에서 시작하는 벡터가 되고 v 벡터는 v1, v2의 좌표를 향하는 원점에서의 벡터로 분홍색으로 표시가 되었습니다. 여기서 v 벡터를 u 벡터에 투영을 한다고 생각을 하고 녹색의 직각의 선을 그어볼 수 있습니다. 그럼 빨간색으로 표현된 길이만큼의 새로운 p가 생깁니다. p 는 v 벡터를 u 벡터에 투영을 하여 생성된 길이를 의미하고 이 값은 + or - 의 값을 가질 수 있습니다.(왼쪽 아래 그래프) 이것을 수식으로 표현을 하면 오른쪽의 파란색으로 표기된 공식과 같이 됩니다.
uT v = p * ||u||
여기서 ||u|| 은 u 벡터의 norm이라고 읽으며 이것은 u 벡터의 euclidean length(Euclidean distance) 로 벡터의 길이를 의미합니다. 이것은 또 ||u|| = SQRT(u1^2 + u2^2) 와 같은 값을 가집니다.
두개의 벡터의 곱하기는 uT v = u1v1+ u2v2 이 되며, 또 이것은 p * ||u|| = u1v1+ u2v2 이 됩니다. 두개의 벡터는 교환법칙이 성립하므로 uT v = vT u도 가능합니다.
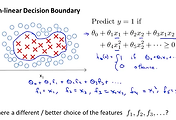
이제 SVM 의 Decision Boundary에 위에서 배운것을 적용해서 생각해보겠습니다. 우선은 간단하게 하기 위해서 세타0 = 0 으로 놓겠습니다.
아래 그림의 위에 공식을 보시면 세타가 1부터 n개까지의 제곱의 합을 1/2 하는 공식이였습니다. 이것을 풀어서 쓰면 1/2( 세타1^2 + 세타2^2)이 되고 이것은 다시 쓰면 1/2 ( 루트 세타1^2 + 세타2^2) 와 같습니다. 위에서 살펴본것과 같이 이것은 세타 벡터의 norm과 같으므로 최종적으로 1/2 ||θ||^2 이 됩니다.
이것을 그래프로 표현하면 아래쪽의 그래프와 같이 됩니다. x 벡터를 세타 벡터에 투영을 하여 생성된 길이 p(i)는 빨간색 선이 됩니다.
(θT xi ) = pi * ||θ|| = θ1xi1 + θ2xi2
y(i)가 1일때는 θT xi의 값이 1보다 크거나 같아야 합니다. 이것은 다시 pi * ||θ|| 가 1보다 크거나 같다는 것과 동일합니다. 반대의 경우도 마찬가지로 y(i)가 0일때는 θT xi의 값이 -1보다 작거나 같아야 하고 이것은 pi * ||θ|| 이 -1보다 작거나 같은 것과 동일합니다. 여기서 p(i)는 x(i)를 세타에 투영하여 생성된 길이를 의미합니다.
왼쪽 아래 그림과 같이 Decision Boundary가 대각선인 경우를 생각해보겠습니다. 이때 직각으로 세타 벡타가 생성이 됩니다. 이 세타 벡터에 각각의 x, o 의 x data 들을 투영해서 생성된 길이 p(i)를 보면 상당히 작은 값을 가진 다는 것을 알 수 있습니다. 이것은 다시 말하면 세타의 norm의 크기가 커야 값이 1 이상의 값을 가질 수 있으며 반대로도 크기가 커야 값이 -1이하의 값을 가질 수 있을 겁니다.
오른쪽 아래 그림과 같이 Decision Boundary가 세로선인 경우를 생각해보겠습니다. 이때 직각으로 세타 벡타가 생성이 되고 거의 x 축과 같이 됩니다. x data들을 투영하여 생성된 길이 p(i)는 보다 큰 값을 가지게 되고 이것은 다시 이야기하면 세타의 norm의 크기가 작아도 되는 결과가 됩니다.
이렇게 p가 커진다는 것은 Decision Boundary와 data간의 거리가 길어지는 것을 의미하며 이 gap이 margin이 됩니다. margin이 크게 형성 되는 Decision Boundary가 좋은 것이라고 할 수 있습니다.
우리는 세타0를 0으로 놓고 살펴보았기 때문에 세타 벡터가 원점을 지나가는 벡터가 되었습니다. 만약 세타0가 0의 값이 아니라면 원점이 아닌 다른 점을 지나가는 벡터가 될 것입니다. 그리고 위에서 알아본바와 동일하게 우리의 알고리즘은 그 지점에서의 margin이 큰 Decision Boundary를 만들게 될 것입니다.
우리가 또 이전에 배웠던 C의 값이 상당히 클 때 CA가 0의 값에 가까워지고 B만 남는 것을 보았습니다. 이러한 가정하에 알아본 것이라는 것을 이해하고 간단하게 살펴보았습니다.
'Machine Learning' 카테고리의 다른 글
| 31. SVM (Support Vector Machine) 사용하기 (0) | 2016.08.15 |
|---|---|
| 30. SVM (Support Vector Machine) - Kernel에 대하여 (0) | 2016.08.14 |
| 28. SVM (Support Vector Machine) - 강력한 classification (4) | 2016.08.09 |
| 27. 머신러닝 시스템을 디자인 하는 방법 (Machine Learning System Design) (4) | 2016.08.06 |
| 26. 머신러닝에서 문제를 해결하는 방안 (6) | 2016.07.27 |






댓글